In search of a definition of uncertainty in three point estimates

I've written elsewhere in this blog about the value and theory of three-point estimating (3PE). See "3PE - why I use three estimates where one might do!". The main practical snag with using 3PE in an agile context is the additional overhead of thinking of 3 numbers every time you want to confirm "effort to complete" - ideally something people can quickly update even on a daily basis.

So I'm working on a mechanism which shows the level of uncertainty in an estimate to complete which takes into account the effort completed to date (T) and the three points of the estimate: best case (b), most likely (m) and worst case (w). If you're interested in the intricacies of such things, please read on!

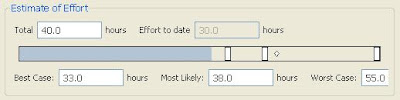The composite estimate (E) is the estimate is the derived "median" which is used when one number is required (as for example in the "Total" field in the screenshot above). It is derived from best case (b), most likely (m) and worst case (w) as follows based on assumptions about distribution of cases between best and worst:

E = (b + 4m + w) / 6

Various formulae are possible for our level of uncertainty or estimate risk (R). Here's a starting point expressed in terms of just b and w as follows:

R = (w - b) / (w + b - 2T) ..................................[1]

This expresses the average "error", (w-b)/2, as a proportion of the average time to complete, (w+b-2T)/2. However since it ignores the most likely estimate, it doesn't take into account that for example the worst case may be much further away from the most likely than the most likely is from the best case. An alternative formula would therefore be:

R = (w - m) / (m -T) ........................................[2]

But this formula ignores the best case completely. One could say the "error" should be defined as whichever is greater out of (w-m) or (m-b), but actually it's not this aspect that worries me practically. The worst case is always more significant from a forecasting viewpoint, and from an estimating viewpoint it is the one that can be much further in error than the best case, which can never go lower than T and in practice will always be a little bit higher than T (or you can forget about estimating and just finish it!).

So a better approach is to define the "error" in the formula for R relative to the median estimate, E, all three points are then taken into account. It's much more satisfactory.

Following this approach, here's the formula for the uncertainty in the estimates (estimate risk) that I'll be using:

R = (w - E) / (E - T) ........................................[3]

For those interested in the mechanisms within xProcess to use this formula, there'll be a discussion on that project's wiki about how users can set estimate to complete and level of uncertainty rather than worrying about 3pe every time they update time to complete.